Steifigkeit und Dämpfung: Das sollten Ingenieure bei der Abstimmung einer Kupplung bedenken

Die Steifigkeit beschreibt den Widerstand eines Körpers gegen elastische Verformung. Ohne Steifigkeit ist die Übertragung von Leistung nicht möglich. Es gibt jedoch Ereignisse, die nicht übertragen werden sollen, etwa Drehmomentspitzen und Stöße. Gegen sie wird ein Antriebssystem gedämpft. Ingenieure stehen vor der Herausforderung in schwingungsfähigen Systemen Steifigkeit und Dämpfung so auszulegen, dass ein möglichst lastspitzenfreier Betrieb gewährleistet ist.
Ein großes und oft unterschätztes Teilgebiet der Technischen Mechanik ist die Schwingungslehre. Zwei hierfür essentielle physikalische Größen sind die Steifigkeit (auch Federsteifigkeit) und die Dämpfung. Die Steifigkeit ist definiert, als der Widerstand eines Körpers gegen eine elastische Verformung. Abhängig von der Belastungsrichtung wird zwischen Zug/Druck-, Biege- und Torsions/Drehfedersteifigkeit unterschieden. Zusätzlich zu der Belastungsrichtung ist die Steifigkeit abhängig vom verwendeten Werkstoff und der Bauteilgestaltung, sprich der Geometrie.
Berechnung der Steifigkeit abhängig von Bauteil-Komplexität und Werkstoffverhalten
Eine Änderung der Steifigkeit in einem schwingungsfähigen System führt neben der Verschiebung der Eigenfrequenzlage zu einer Änderung der Periodenlänge einer Schwingung (vgl. Abb. 1).
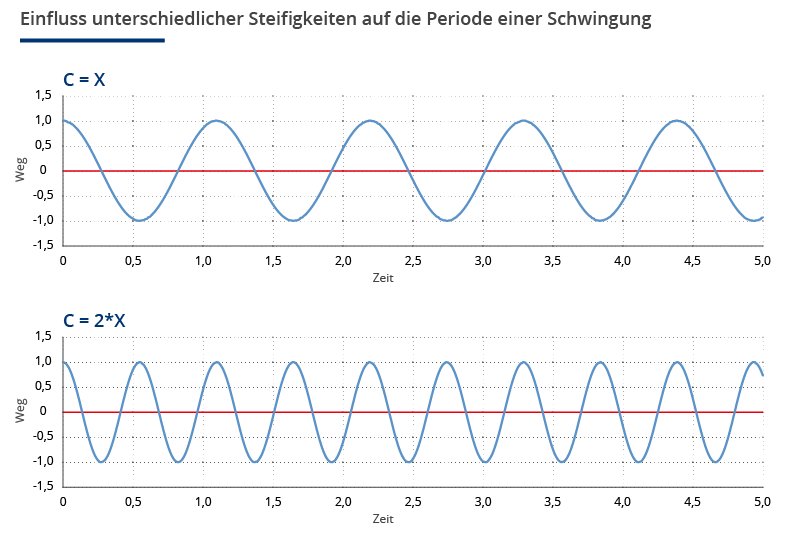
Abb. 1 Einfluss unterschiedlicher Steifigkeiten auf die Periode seiner Schwingung.
So kann für einfache Geometrien (etwa Stabelemente) und sich abschnittsweise linear verhaltende Werkstoffe die Steifigkeit über feststehende Formeln berechnet werden. Bei komplexeren Bauteilen oder nicht linearem Materialverhalten (etwa Elastomeren) wird neben höheren Berechnungsverfahren häufig auch die Finite-Elemente-Simulation zur Bestimmung der Steifigkeit verwendet.
Die Dämpfung ist rein werkstoffabhängig
Im Gegensatz zur Steifigkeit ist die Dämpfung eine Werkstoffkenngröße und kann im Allgemeinen nicht über die Formgebung eines Bauteils beeinflusst werden. Die Dämpfung beschreibt die von einem schwingenden System abgeführte Energie (meist als Wärme) und verursacht damit ein Abklingen der Schwingungsamplitude über der Zeit (vgl. Abb. 2).
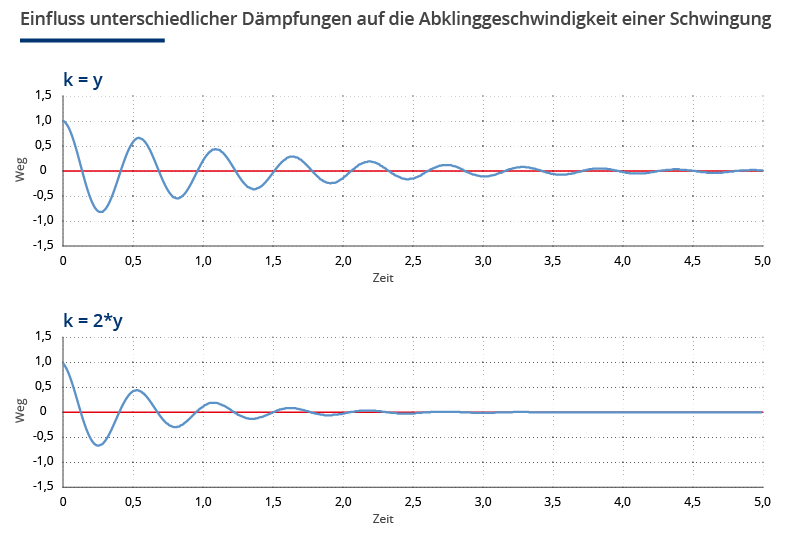
Abb. 2: Einfluss unterschiedlicher Dämpfungen auf die Abklinggeschwindigkeit einer Schwingung.
Herausforderung Schwingung in ungleichförmigen Antrieben
Im Gegensatz zu Antrieben mit gleichförmigem Drehmomentverlauf (z. B. mit einem Elektromotor) treten in Antriebssträngen mit Verbrennungsmaschinen (wie z. B. Kolbenmotoren) ungleichförmige Drehmomentverläufe mit periodischer Anregung und dynamisch überlagerten Amplituden auf, die die Aggregate stark beanspruchen. Diese „dynamischen Störungen“ machen sich in Form von Drehschwingungen im Antriebsstrang bemerkbar. Die Ursache hierfür ist die periodische Anregung durch die beim Verbrennungs-/Zündvorgang entstehenden Gas- und Massenkräfte. Ein Dieselmotor etwa gibt seine Leistung nicht gleichmäßig während einer Umdrehung der Kurbelwelle ab. Die unstetigen Drehmomentverläufe der einzelnen Zylinder eines Kolbenmotors überlagern sich in ihrer Zündreihenfolge und den möglicherweise ungleichmäßigen Zündabständen zu einer periodisch wirkenden Anregung, die die Kurbelwelle in Drehschwingungen versetzt.
Zu einem Resonanzproblem kommt es, wenn das System periodisch mit einer Frequenz angeregt wird, die mit der des Systems (der sogenannten Eigenfrequenz) übereinstimmt. Hierdurch nimmt die Amplitude der Schwingung fortlaufend zu. Das System schaukelt sich auf, es befindet sich in Resonanz. Stimmt die Frequenz dieser Anregung mit einer der Eigenfrequenzen des Systems überein, spricht man von einem Resonanzfall. Die Schwingungsamplituden können dann nicht mehr gedämpft werden, sondern sie werden im Gegenteil immer größer.
Steifigkeit und Dämpfung in Antrieben mit ungleichförmigen Drehmoment
Antriebe mit ungleichförmigen Drehmoment haben daher besonders hohe Anforderungen sowohl an die Steifigkeit wie die Dämpfung. Um diesen Anforderungen gerecht zu werden, werden drehelastische Kupplungen eingesetzt, die Drehschwingungsamplituden und Drehmomentstöße ausgleichen.
Bei dynamisch nicht abgestimmten Systemen kann es leicht zu Schäden kommen. Diese entstehen, wenn Drehmomentspitzen oder Drehmomentstöße das System oder Teile des Systems über die zulässigen Werte beanspruchen. Das können akute Materialschäden wie ein Bruch sein, aber auch ein starker Abrieb und somit ein schnellerer Verschleiß.
Erst mit der Sicherstellung eines dynamisch abgestimmten Verhaltens des gesamten Antriebsstrangs, das sowohl die Vermeidung von Resonanzstellen im Betriebsbereich, die Dämpfung von Schwingungen und Drehmomentstößen beinhaltet, sowie dem Ausgleich von geometrischen Versätzen, wird ein sicherer und performanter Betrieb des Systems sichergestellt und eine Erhöhung der Lebensdauer der gesamten Anlage erreicht.
Glossar
Steifigkeit
Die Steifigkeit ist ein Begriff der technischen Mechanik. Sie beschreibt den Widerstand eines Körpers gegen elastische Verformung, der durch äußere Einwirkung, wie Kraft oder Drehmoment, hervorgerufen wurde.
Festigkeit
Steifigkeit darf nicht mit der Festigkeit verwechselt werden. Die Festigkeit, beispielsweise die Zugfestigkeit, ist ein Grenzwert, der beschreibt, wie groß die ertragbare Belastung eines Werkstoffs ist. Er steht in keiner Abhängigkeit zur Steifigkeit.
Resonanz
Wird ein schwingungsfähiges System periodisch angeregt, schaukelt es sich auf. Dieses Phänomen nennt man Resonanz. Die Voraussetzung: Die Frequenz des Erregers und des Systems sind gleich oder nahezu gleich.


Kommentieren